retour
ANNEXE 1
Etude détaillée de l'extinction
Voir la figure 28.

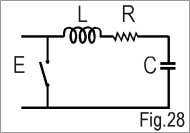
Dans cette figure, nous pouvons écrire que l'énergie fournie par la source est égale à l'énergie emmagasinée plus l'énergie dissipée dans le circuit.

énergie fournie
pendant le temps dt :
Eidt
 =
Pertes JOULE
dans R :
Ri2dt
 +
énergie
électrostatique
d(QV)
 +
énergie
électromagnétique
di
Où Q est la charge emmagasinée dans le condensateur soumis à une tension V.
est le flux produit par le courant i dans la self L
Dans le condensateur, la quantité dq emmagasinée pendant le temps dt vaut : dq = idt et Q = idt = CV
d'où l'on tire V = Q / C ou encore, en multipliant par Q :
  qui, différentié donne : d(QV) = (2Q/C)dq

et d(1/2 QV) = 1/C.Qdq = Q/C dq = Vdq

et avec dq = idt, on a évidemment : d(1/2 QV) = Vidt
Pour la bobine, nous avons = Li donc di = Lidi

L'équation générale devient : Eidt = ri2dt + Vidt + Lidi

que l'on divise par idt : E = ri + V + L (di/dt)

d'autre part, pour une capacité, on a : i = C (dv/dt)

En différentiant une seconde fois, on a : di/dt = C (d2v / dt2), ce qui entraîne :
équation différentielle générale du deuxième ordre d'un circuit RLC.
Lorsque l'interrupteur est basculé, court-circuitant le générateur, l'équation se réduit à :
 
dont l'équation caractéristique est 0 = LCx2 + RCx + 1, et l'intégrale générale de cette équation différentielle a la forme :
v = C1ex1t + C2ex2t
ou C1 et C2 sont les constantes d'intégration, définies par les conditions initiales, et x1 et x2, les solutions de l'équation caractéristiques, sont :

Si on pose :
Les solutions x1 et x2 deviennent :
Analyse en fonctionnement

Conditions initiales : Interrupteur ouvert, courant nul dans L, C chargé à E.
1er temps

Immédiatement après la fermeture de l'interrupteur, le courant commence à s'établir et croît progressivement. Pendant ce premier temps, R est faible et L est grand (self non saturée).
Le discriminant de l'équation caractéristique est fortement négatif       R2C2 - 4 LC < 0.
Le terme R2C2 est très inférieur à 4LC et peut être négligé en première approximation.

Alors, = -1/LC = -2        et les racines :
Les racines sont alors imaginaires conjuguées :
x1 = - + j        et        x2 = - - j
La solution générale devient :
v = C1e(- - j)t + C2e(- + j)t
que l'on développe en :
v = C1e-t . e- jt + C2e-t . ejt
v = e-t (C1e- jt + C2ejt)
D'autre part, on démontre que ej = cos + j sin
donc :
v = e-t [C1 cos (-t) + jC1 sin (-t) + C2 cos t + jC2 sin t]
v = e-t [(C1 + C2) cos t + j(C1 - C2) sin t]
Mais il est nécessaire que v soit réel. Ceci implique que (C1 + C2) et (C1 - C2) soient réels simultanément. Cette condition est réalisée si C1 et C2 sont des imaginaires conjugués.
C1 = a + jb et C2) = a - jb
C1 + C2 = 2a = A et j(C1 - C2) = j(2jb) = -2b = -B
On a alors :
v = e-t [A cos t - B sin t]
Les conditions initiales, avant la fermeture de l'interrupteur sont : Vo = E, Io = 0, donc pour t = 0, il reste:
v = e-t [A . 1 - B . 0] = Vo
c'est-à-dire :      A = Vo = E.
donc        v = E.e-t [cos t - B/E sin t]
L'intensité est obtenue après différentiation de v, car i = C dv/dt
on a donc
dv/dt = e-t [(E + B) sin t - (E - B) cos t]
et enfin
i = C dv / dt = C.e-t [(E + B) sin t - (E - B) cos t]
Pour t = 0, on doit avoir Io = 0
i = C. 1 [(E + B). 0 - (E - B). 1] = 0        ( e0 = 1, sin 0 = 0, cos 0 = 1)
Il faut alors :       E = B
c'est-à-dire :       B = E /
En conclusion, v et i deviennent:
v = E.e-t [ cos t + / sin t ]        (1)
i = C.E.e-t . ( 1 + 2 / 2) sin t       (2)

La tension v et le courant i, immédiatement après la fermeture du circuit, évoluent suivant le début d'une oscillation sinusoïdale amortie, dont la période T = 2 / vaut:       ( défini plus haut)

             ( Rappel : R2C2 << 4LC)
la très classique loi de Thomson

Les valeurs des composants L et C donnent une période T longue. Le courant croît alors suivant un arc sinusoïde, jusqu'au moment où ce courant atteint la valeur de saturation de la self saturable. Le temps t1 qui s'est écoulé entre le début du fonctionnement, et l'instant où le courant i atteint celui de la saturation de la self, dépend évidemment de la valeur de ce courant de saturation, de la période T, et de l'amplitude maximum théorique de i, qui elle-même dépend de E.

Ce temps t1, pour une tension E de 1500 V est d'environ 500 s.

2ème temps : 1ère saturation de L

500 s après la fermeture de l'interrupteur, le noyau de la self atteint la saturation; c'est-à-dire que la valeur de l'inductance tombe à une faible valeur (R reste néanmoins faible par rapport à L). A partir de cet instant, la loi d'accroissement reste la même dans sa forme, mais la période T1 est fortement réduite, et prend la valeur T2.

Le courant croît jusqu'à une valeur de 200 A environ, puis décroît suivant une loi sinusoïdale ( période). Simultanément, la tension aux bornes du condensateur tombe à zéro quand le courant est maximum, puis s'inverse, le tout suivant une loi cosinusoïdale.

La valeur de R est telle que le coefficient d'amortissement est réduit, c'est-à-dire que la tension aux bornes du condensateur qui était de +E,
atteint (-E + ) en fin de période (T2) (figure 7).

Le courant i a augmenté jusqu'à une valeur élevée, puis est redescendu jusqu'à la valeur de saturation. A cet instant t2, la self se déssature, et le cycle continu avec la période T1, pendant 500 s. A cet instant t3, le courant est nul, et la tension sur le condensateur a atteint -E.

L'oscillation se poursuit, le courant s'inverse, la tension sur C est revenue à (-E + ).
3ème temps : 2ème saturation de L

Au bout de ce troisième délai de 500 s, le courant i atteint la valeur de saturation opposée, et le même cycle se reproduit : le courant augmente vers -200 A suivant la même loi que précédemment, et la tension du condensateur est à zéro quand i = Imax.

Faisons intervenir maintenant le circuit réel. Dans celui-ci, l'interrupteur est remplacé par un thyristor Th1 et une diode en inverse, D4 (figure 6)

Pendant le 2ème temps, i avait le même sens que le courant principal Ic, et pendant ce 3ème temps, i est dans le sens inverse du courant Ip.

Les éléments sont tels que les valeurs absolues répondent à l'inéquation suivante :

|i| >> |Ic|
Le courant s'annule dans le thyristor et celui-ci se désamorçe; le courant i continu de circuler par la diode D4; le cycle se termine ainsi.

4ème temps : déssaturation de L

Lorsque i devient inférieur à l'intensité de saturation, la self se déssature, et le cycle se termine avec la période T1. Lorsque ce courant est nul, la diode se bloque, et comme le thyristor est bloqué, l'oscillation s'arrête, et les conditions initiales sont rétablies : V cond. = +E, th bloqué.

Le temps de conduction du thyristor est celui qui s'est écoulé depuis le début du cycle (début de la décharge de Cc), jusqu'à la deuxième saturation de la self Lc, au moment où le courant de charge de Cc atteint la valeur du courant principal traversant le thyristor en direct.

étant donné que le temps entre le passage par 0 du courant dans le circuit Lc-Cc, et le début de la saturation est une fonction inverse de E (équation 2), le temps de conduction de Th sera aussi une fonction quasi linéaire de E, puisque on travaille uniquement sur le début d'une sinusoïde (voisinage de 0).
Donc, quand E augmente, t1 diminue : t1 = K/E .

   Sommaire / description - puissance Annexe 1 originale 1969 en pdf