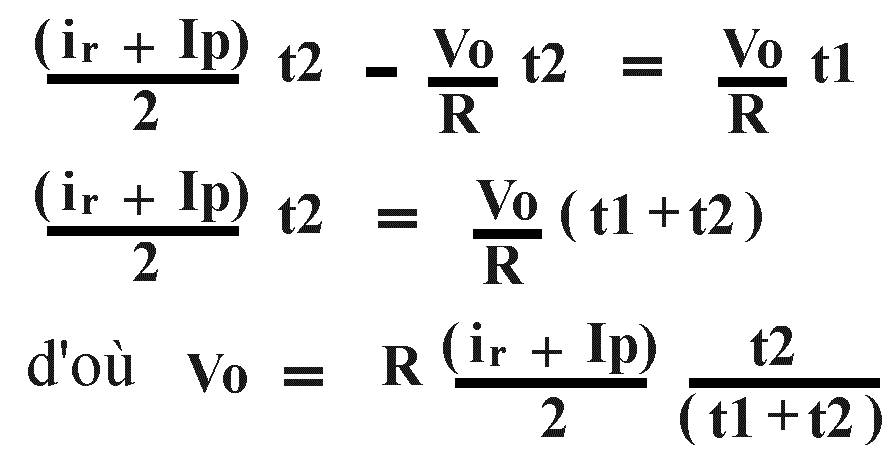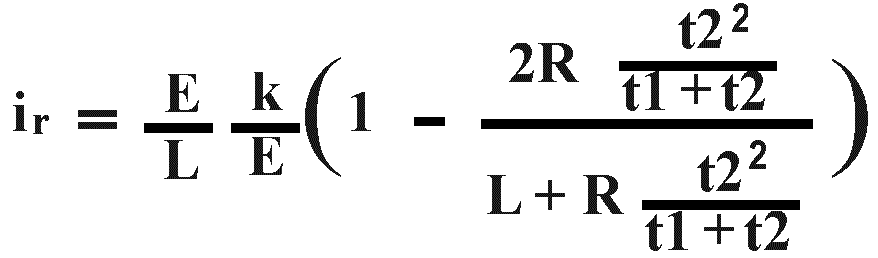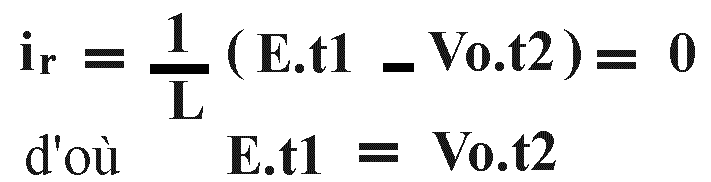ANNEXE 2

Ce circuit est constitué (figure 9), par les éléments Cp Rp , D2 et D3, mais les éléments du circuit d'extinction et Cf participent aussi à la démagnétisation, tout au moins au début de celle~ci. La démagnétisation a pour but d'offrir un chemin au courant qui doit continuer de circuler dans Lp, après 1'ouverture de Th, courant dû à l'énergie magnétisante emagasinée durant la période de conduction du thyristor.

Plaçons nous donc au temps to, où le thyristor vient, juste de se bloquer, c'est-à-dire que le courant Ic, d'extinction est dans la phase croissante du 3ème temps décrit en annexe 1, et sa valeur est égale et opposée au courant Ip. Ic se ferme alors par D4, et le courant Ip peut se poursuivre pendant le temps de la recharge de Cc, par Lc, Cc et Cf. C'est le courant I1 de la figure 9, mais dès que Cc est recharge; le courant Ip qui traversait la self Lc y a créé une énergie magnétisante, et Ip doit s'écouler pendant un certain temps dans Lp. Ce courant est le même, au début du cycle que celui qui circule dans Lc. En début de cycle, le courant dans Lc se boucle par D3, Cp , Lp, D1, mais au bout d'un certain temps, le courant Ip devient supérieur au courant dans Lc, à ce moment, la diode D2 commence à conduire et est traversée alors par la différence entre ILc et Ip. Le courant ILC se boucle alors par D3, D2, D4. Quand Thi s'ouvre, l'inductance Lp qui se comportait comme un récepteur, se comporte alors comme un générateur, et le courant qui la traverse n'ayant pas changé de sens, c'est la tension à ses bornes qui s'inverse. Cette tension était E = L(di/dt) et elle devient - V = L(di/dt) car le courant décroît et di/dt est négatif.

Ce circuit oscillant comporte une résistance shunt.

On a : I_L = Ic + I_R
avec I_R = v / R
et Ic = C.dv/dt    d'où I_L = v / R + C.dv/dt

Différencions cette solution par rapport au temps : dans laquelle di/dt vaut, d'après        -v = L.di/dt :

di/dt = - (v/L)

Ce qui donne :

soit, en multipliant par RL:

La forme de la solution sera identique à celle que nous avons déjà trouvé, avec néanmoins = -1/RC, et :

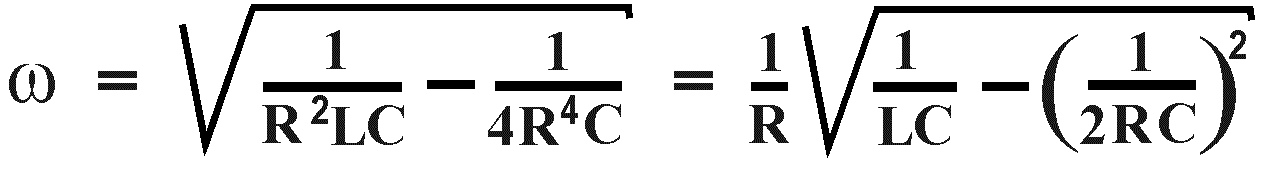v = Vo + e^-t( A cos t - B sin t)

avec pour t = 0, v = Vo :

v = Vo + 1.(A.1 - B.0) d'où A = 0
et v = Vo - Be^-t sin t    (3)

Nous remarquons que la valeur de est particulièrement faible, étant donné que C, qui apparaît deux fois, est très élevé (370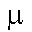F).
En conséquence, la période T = 2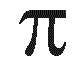 / sera longue, et dans un interval de temps t réduit devant T, la tension v n'aura pratiquement pas bougé. Si nous supposons la tension v quasiment constante, on peut dire :

• que le courant traversant la résistance est constant
• que le courant traversant la self décroît linéairement de Ip à une valeur i qui dépend du temps
• enfin, que le courant dans le condensateur suit le courant I_L, à une constante I_R près.

Puisque I_R = Vo / R, plus Vo est faible, plus I_R est faible.
A la limite, lorsque Vo est nul, c'est-à-dire au démarrage du convertisseur, le courant dans R est nul, et Ic = I1. Si Vo est faible, I_R est faible, et le condensateur accumule des charges.

La quantité d'électricité perdue par le condensateur pendant le temps t1 de conduction du thyristor est q = I₁.t1 = (Vo / R)t1.
La quantité d'électricité libérée par la self Lp pendant le temps de blocage du thyristor sera, si Ip est l'intensité au moment du blocage de Th, et i_r l'intensité à l'instant du réamorçage de Th, et t2 le temps écoulé entre ces deux instants, on a :

q1 = t2.(i_r + Ip) / 2

Et la quantité q2 reçue par le condensateur sera :

q1 = (t2.(i_r + Ip) / 2) - t2.(Vo / R)

Le montage sera équilibré quand q1 = q2 :

Ip est l'intensité à l'instant de l'ouverture de Th1. Elle dépend donc du temps de conduction t1 du thyristor, et de la tension caténaire E; Ip = (E.t1) / L, en supposant nul le courant initial. Ce cas se produit au démarrage du convertisseur. On a alors :

En régime établi, le courant Ip ne s'annule jamais, et I_r existe et vaut pour 1 période:

Ce qui donne :

On voit que Vo est fonction de E, tension ligne, et des temps de conduction et de blocage du thyristor.
La valeur du courant résiduel i_r:

Donc, i_r serait une fonction linéaire de E, mais nous avons vu à la fin du paragraphe sur l'extinction, que le temps t1 de conduction est une fonction inverse de E : t1 = k / E

Dans la parenthèse, R est très grand devant L. On peut donc négliger L et il devient :

i_r ne dépend donc, ni de E, ni de t1 / t2 en première approximation.

Ce courant i_r est le courant circulant encore dans le self primaire juste avant l'allumage du thyristor, et est égal à l'amplitude de la variation d'intensité pendant t1 : E.t1 / L , moins l'amplitude de l'intensité de démagnétisation (Vo / L)t2

Après la première période, le courant max. (ou de pointe effectivement absorbé) est après la fin de la deuxième conduction de Th1 :

Imax2 = i_r + (E.t1 / L)

La démagnétisation laisse circuler, après la fin de la deuxième période, un courant :

Après le temps t1 de la 3ème période, le courant Imax atteint :

Imax3 = 2i_r + (E.t1 / L)

Après la démagnétisation, à la fin de la 3ème période, le courant résiduel sera de 3i_r, et ainsi de suite, i_r indiquant la valeur absolue du courant résiduel, celle que l'on mesure par rapport à l'origine. Mais le phénomène que nous allons expliquer intervient, pour stabiliser le fonctionnement.

L'énergie emmagasinée dans le noyau pendant la croissance du courant est : w = I d, où d est la variation du flux, et I la variation de courant. Si l'on considère la courbe d'induction d'un noyau magnétique, que nous supposerons sans hystérésis (fig. 10), on constate, que lorsque l'intensité résiduelle augmente, la variation d'intensité pendant la conduction de Th restant presque constante, l'augmentation de et, par conséquence de tend à diminuer, d'une période à la suivante, à cause de la saturation du noyau. Ceci signifie, que l'énergie stockée pendant une conduction par rapport à la précédente, diminue. Mais l'amplitude de la variation du courant de démagnétisation reste pratiquement constante, et est liée à Vo, donc 1'énergie récupérée par la capacité reste pratiquement constante. En conséquence, après un certain nombre de périodes Imax atteint une valeur telle que 1' énergie restituée égale l'énergie emmagasinée,c'est-à-dire que le courant résiduel ir d'une période à l'autre tend vers 0.

Il résulte de l'équation (4) que 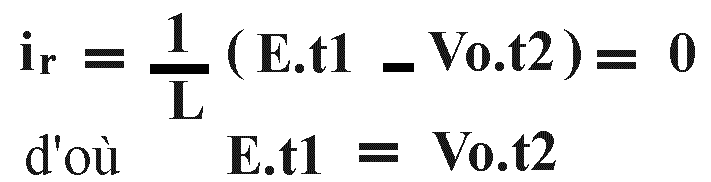Autrement dit, si l'on prend une considération géométrique (fig.11) les surfaces E.t1 et Vo.t2 sont égales, condition de stabilité de fonctionnement.

---

Sommaire / description - puissance

Annexe 2 originale 1969 en pdf